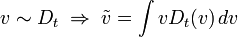กิจกรรม 17-21 มกราคม 2554


สืบค้นข้อมูล

การเคลื่อนที่ (อังกฤษ: motion) คือ การเปลี่ยนตำแหน่งของวัตถุในช่วงเวลาหนึ่ง ซึ่งวัดโดยผู้สังเกตที่เป็นส่วนหนึ่งของกรอบอ้างอิง เมื่อปลายคริสต์ศตวรรษที่ 19 เซอร์ไอแซก นิวตัน ได้เสนอกฎการเคลื่อนที่ของนิวตันในหนังสือ Principia ของเขา ซึ่งต่อมาได้กลายเป็นกฎพื้นฐานของฟิสิกส์ดั้งเดิม การคำนวณการเคลื่อนที่ของวัตถุต่างๆ โดยใช้ฟิสิกส์ดั้งเดิมนั้นประสบความสำเร็จมาก จนกระทั่งนักฟิสิกส์เริ่มศึกษาเกี่ยวกับสิ่งที่เคลื่อนที่ด้วยความเร็วสูงมาก
นักฟิสิกส์พบว่า ฟิสิกส์ดั้งเดิมไม่สามารถคำนวณสิ่งที่เคลื่อนที่ด้วยความเร็วสูงได้แม่นยำ เพื่อแก้ปัญหานี้ อองรี ปวงกาเร และ อัลเบิร์ต ไอน์สไตน์ได้เสนอทฤษฎีอธิบายการเคลื่อนที่ของวัตถุ เพื่อใช้แทนของกฎของนิวตัน กฎการเคลื่อนที่ของนิวตันกำหนดให้อวกาศและเวลาเป็นสิ่งสัมบูรณ์ แต่ทฤษฎีไอน์สไตน์กับปวงกาเร ซึ่งเรียกว่า ทฤษฎีสัมพัทธภาพพิเศษ กำหนดให้ค่าเหล่านี้เป็นสิ่งสัมพัทธ์ ซึ่งต่อมา ทฤษฎีสัมพัทธภาพพิเศษก็เป็นที่ยอมรับในการอธิบายการเคลื่อนที่ เพราะทำนายผลลัพธ์ได้แม่นยำกว่า อย่างไรก็ตาม ในทางปฏิบัติ กฎการเคลื่อนที่ของนิวตันยังเป็นที่ใช้กันอยู่ โดยเฉพาะงานด้านฟิสิกส์ประยุกต์และงานวิศวกรรม เพราะสามารถคำนวณได้ง่ายกว่าทฤษฎีสัมพัทธภาพพิเศษ

ตอบ ข้อ 3.

ที่มา http://th.wikipedia.org/wiki/%E0%B8%81%E0%B8%B2%E0%B8%A3%E0%B9%80%E0%B8%84%E0%B8%A5%E0%B8%B7%E0%B9%88%E0%B8%AD%E0%B8%99%E0%B8%97%E0%B8%B5%E0%B9%88


สืบค้นข้อมูล

ในขณะที่วัตถุมีการเคลื่อนที่  ได้ระยะทางและการกระจัดในเวลาเดียวกัน  และต้องใช้เวลาในการเคลื่อนที่  จึงทำให้เกิดปริมาณสัมพันธ์ขึ้น  ปริมาณดังกล่าวคือ
    1. อัตราเร็ว  คือ ระยะทางที่วัตถุเคลื่อนที่ได้ในหนึ่งหน่วยเวลา จัดเป็นเปริมาณสเกลลาร์ หน่วยในระบบเอสไอ มีหน่วยเป็น เมตร/วินาที
    2. ความเร็ว คือ ขนาดของการกระจัดที่วัตถุเคลื่อนที่ได้ในหนึ่งหน่วยเวลา จัดเป็นปริมาณเวกเตอร์ ใช้หน่วยเดียวกับอัตราเร็ว
    สมการแสดงความสัมพันธ์ของอัตราเร็ว ระยะทาง และเวลาเป็นดังนี้           ให้         เป็นค่าอัตราเร็วหรือความเร็ว                        เป็นระยะทางหรือการกระจัด                         เป็นเวลาที่ใช้ในการเคลื่อนที่            สมการคือ                           (สมการที่ 1)                  
         อัตราเร็ว และความเร็ว เป็นปริมาณที่แสดงให้ทราบลักษณะการเคลื่อนที่ของวัตถุ    ถ้าในทุก ๆ  หน่วยเวลาของการเคลื่อนที่วัตถุเคลื่อนที่ด้วยขนาดของอัตราเร็ว หรือ ความเร็วเท่ากันตลอดการเคลื่อนที่ เรียกว่าวัตถุเคลื่อนที่ด้วยอัตราเร็วสม่ำเสมอหรืออัตราเร็วคงที่         ถ้าพิจราณาแล้วพบว่าในแต่ละหน่วยเวลาของการเคลื่อนที่วัตถุเคลื่อนที่ด้วยอัตราเร็วหรือความเร็วที่แตกต่างกัน กล่าวว่า วัตถุเคลื่อนที่ด้วยอัตราเร่ง หรือ ความเร่ง   ในกรณีนี้การหาค่าอัตราเร็วหรือความเร็ว หาได้สองลักษณะคือ
    1. อัตราเร็วขณะใดขณะหนึ่ง หรือความเร็วขณะใดขณะหนึ่ง เป็นการหาค่าอัตราเร็วหรือความเร็วในช่วงเวลาสั้น ๆ ช่วงใดช่วงหนึ่งของการเคลื่อนที่ 
    2. อัตราเร็วเฉลี่ยหรือความเร็วเฉลี่ย เป็นการหาค่าอัตราเร็วหรือความเร็วหลังจากมีการเคลื่อนที่  โดยคำนวณหาจากการเฉลี่ยระยะทางทั้งหมดของการเคลื่อนที่ในหนึ่งหน่วยเวลาของการเคลื่อนที่ หรือการเฉลี่ยการกระจัดของการเคลื่อนที่ในหนึ่งหน่วยเวลา     
    ข้อสังเกต   วัตถุที่เคลื่อนที่ด้วยอัตราเร็วสม่ำเสมอ ค่าอัตราเร็วขณะใดขณะหนึ่ง กับค่าอัตราเร็วเฉลี่ยมีค่าเท่ากัน
ตอบ ข้อ 2. 10 m/s

ที่มา http://www.snr.ac.th/elearning/kosit/sec02p01.html



สืบค้นข้อมูล





กาลิเลโอ ได้ทำการทดลองให้เห็นว่า วัตถุที่ตกลงสู่พื้นโลกอย่างอิสระ จะเคลื่อนที่ภายใต้แรงดึงดูดของโลก ต่อมานิวตันสังเกตุเห็นว่า ทำไมดวงจันทร์ไม่ลอยหลุดออกไปจากโลก ทำไมผลแอปเปิ้ลจึงตกลงสู่พื้นดิน นิวตันได้ทำการศึกษาค้นคว้าต่อ จนในที่สุดก็สามารถพิสูจน์ในเรื่องกฎแห่งการดึงดูดของ สสาร โดยโลกและดวงจันทร์ต่างมีแรงดึงดูดซึ่งกันและ กัน แต่เนื่องจากดวงจันทร์โคจรรอบโลก จึงมีแรงหนีสู่ศูนย์กลางซึ่งต่อต้านแรงดึงดูดไว้ ทำให้ดวงจันทร์ลอยโคจรรอบโลกได้ แต่ผลแอปเปิ้ลกับโลกก็มีแรงดึงดูดระหว่างกัน ผลแอปเปิ้ลเมื่อหลุดจากขั้วจึงเคลื่อนที่อิสระตามแรงดึงดูดนั้น
การตกอย่างอิสระนี้ วัตถุจะเคลื่อนตัวด้วยความเร่ง ซึ่งเรียกว่า Gravitational acceleration หรือ g ซึ่งมีค่าประมาณ 9.8 m/s
การเคลื่อนที่ในแนวดิ่งนี้จึงเป็นไปตาม กฎการเคลื่อนที่ ดังนี้


ตอบ ข้อ 4. 49 m/s
ที่มา http://web.ku.ac.th/schoolnet/snet3/kung/vertic_move/vertic_m.htm




สืบค้นข้อมูล

 การเคลื่อนที่แบบฮาร์โมนิกอย่างง่าย



คือการที่วัตถุเคลื่อนที่กลับไปมาซ้ำรอยเดิม มักจะใช้สัญญลักษณ์ว่า SHM. ตัวอย่างของการเคลื่อนที่แบบนี้ได้แก่ การเคลื่อนที่ของวัตถุที่ถูกผูกติดไว้กับสปริงในแนวราบ แล้ววัตถุเคลื่อนที่ไปมาตามแรงที่สปริงกระทำต่อวัตถุ ซึ่งเขาจะศึกษาการเคลื่อนที่นี้จากรูปที่ 1
ในรูปที่ 1a ตำแหน่ง x = 0 เป็นตำแหน่งสมดุลของปริง หรือ เป็นตำแหน่งที่สปริงมีความยาวตามปกติ ณ ตำแหน่งนี้สปริงจะไม่ส่งแรงมากระทำต่อวัตถุ ในรูปที่ 1a นี้มีวัตถุมวล m ผูกติดกับสปริง วางอยู่บนพื้นที่ซึ่งไม่มีแรงเสียดทาน ที่ตำแหน่งซึ่งปริงยืดออกจากความยาวปกติเป็นระยะทาง A สปริงจะออกแรงดึงวัตถุมวล m กลับมาอยู่ในตำแหน่งสมดุล x = 0 เรียกแรงที่สปริงกระทำต่อวัตถุนี้ว่าแรงดึงกลับ (Restoring force) ถ้า F เป็นแรงดึงกลับนี้จะได้ว่า
F = -kx -----(1)
แรงดึงกลับมีเครื่องหมายลบ เพราะทิศทางของเวกเตอร์ของแรงกับเวกเตอร์ของการขจัด x มักจะตรงข้ามกันเสมอ ค่า k คือค่านิจของสปริง (spring constant) ในรูปที่ 1 นี้ได้กำหนดให้ทิศทางขวาเป็นบวก ดังนั้นในรูป 1a ตำแหน่ง x = A จึงเป็นบวก ในขณะที่ทิศทางของแรงดึงกลับเป็นลบ และเนื่องจากวัตถุเริ่มเคลื่อนที่ที่ x = A ความเร็วของวัตถุจึงเป็นศูนย์
เมื่อปล่อยให้วัตถุเคลื่อนที่ตามแรงของสปริง วัตถุจะเคลื่อนที่มาทางซ้าย และในรูปที่ 1b วัตถุผ่านตำแหน่ง x = 0 หรือตำแหน่งสมดุลซึ่งตำแหน่งนี้ แรงที่สปริงกระทำต่อวัตถุจะเป็นศูนย์ แต่อัตราเร็วของวัตถุจะมากที่สุด โดยทิศของความเร็วจะเป็นจากขวาไปซ้าย หรือความเร็วเป็นลบ เนื่องจากพื้นไม่มีแรงเสียดทาน และสปริงก็ไม่ออกแรงมากกระทำต่อวัตถุ ดังนั้นที่ตำแหน่ง x = 0 นี้ วัตถุจึงสามารถรักษาสภาพการเคลื่อนที่ตามกฎข้อที่ 1 ของนิวตันไว้ได้ วัตถุจึงยังคงสามารถเคลื่อนที่ต่อไปทางซ้ายได้
ในขณะที่วัตถุเคลื่อนที่ไปทางซ้ายนั้น วัตถุก็จะผลักให้สปริงหดสั้นไปจากความยาวเดิมด้วย ดังนั้นสปริงจะพยายามออกแรงดึงกลับไปกระทำต่อวัตถุ เพื่อให้ตัวเองกลับไปสู่ความยาวปกติอีก จนในรูปที่ 1 C แสดงถึงขณะที่วัตถุเคลื่อนที่ไปทางซ้ายมากที่สุด ความเร็วของวัตถุจะเป็นศูนย์ทิศของแรงดึงกลับจากซ้ายไปขวา หรือเป็นบวก เวกเตอร์ของการขจัดของวัตถุมีทิศจากขวาไปซ้าย และมีขนาดเป็น A ดังนั้นตำแหน่งของวัตถุขณะนี้จึงเป็น x = -A มีข้อน่าสังเกตว่า ขนาดของการขจัดมากที่สุดของวัตถุไม่ว่าจะเป็นทางซ้ายหรือขวาจะเท่ากัน คือเป็น a เนื่องจากในรูป 1c นี้มีแรงมากระทำต่อวัตถุเพียงแรงเดียว คือแรงจากสปริง ซึ่งมีทิศไปทางขวา วัตถุจึงเคลื่อนที่กลับไปทางขวาด้วยอิทธิพลของแรงนี้


รูปที่ 1
ในรูป 1d วัตถุกลับมาที่ตำแหน่งสมดุลของสปริงอีกครั้งหนึ่ง เช่นเดียวกับในรูป 1b แต่ในขณะนี้วัตถุมีความเร็วเป็นบวก หรือไปทางขวาวัตถุจึงยืดสปริงออกไป โดยยืดได้มากที่สุดถึงตำแหน่ง x = A ดังแสดงในรูป 1 e ซึ่งเป็นสถานเดียวกับรูป 1a ดังนั้นการเคลื่อนที่ของวัตถุจึงกลับมาในลักษณะเดิม คือจาก 1a 1b 1c 1d 1e 1a เป็นอย่างนี้เรื่อยไป ซึ่งจะเห็นว่าวัตถุมีการเคลื่อนที่กลับไปมาซ้ำของเดิม จึงเป็นการเคลื่อนที่แบบ SHM. มีข้อพึงระลึก จากสมการที่ (1) หรือ F = -kx ว่า วัตถุที่เคลื่อนที่แบบ SHM นั้น นอกจากจะเคลื่อนที่กลับไปมาซ้ำรอยเดิมแล้ว แรงดึงกลับที่กระทำต่อวัตถุยังแปรผันโดยตรงกับการขจัดของวัตถุอีกด้วย
ในการศึกษาการเคลื่อนที่แบบ SHM นี้ จะต้องกำหนดปริมาณต่าง ๆ ดังต่อไปนี้
การขจัด (dis placement) คือระยะทางที่วัตถุเคลื่อนที่ไปได้โดยนับจากจุดสมดุล
อัมปลิจูด (amplitude) คือระยะทางมากที่สุดที่วัตถุจะสามารถเคลื่อนที่ไปได้ โดยนับจากจุดสมดุลเช่นเดียวกัน อาจจะพิจารณาได้ว่าอัมปลิจูด ก็คือการขจัดมากที่สุดนั่นเอง
คาบ (period) คือเวลาที่วัตถุใช้ในการสั่น 1 รอบ (เช่นจากรูป 1a ถึง 1e
ความถี่ (frequency) คือจำนวนรอบที่วัตถุสั่น หรือเคลื่อนที่ได้ใน 1 วินาที จากนิยามเหล่านี้ ถ้า f เป็นความถี่ และ T เป็นคาบ จะได้ว่า
T =


ตอบ 3. 4 s

ที่มา http://web.ku.ac.th/schoolnet/snet3/supinya/harmonic-mot/harmonic.htm

สืบค้นข้อมูล
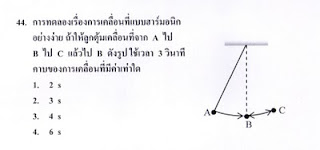
ในการทดลองคาบการแกว่งของลูกตุ้มอย่างง่าย Simple Pendulum
จากกฎข้อที่ 2 ของนิวตัน(เชิงมุม) จะได้ (mL^2)*a = -mgLsin(q), a เป็นความเร่งเชิงมุม อนุพันธ์อันดับสองของมุม q
สำหรับกรณีมุม theta เล็กๆ จะได้ว่า คาบการสั่น T = 2pi sqrt(L/g)
แม้ว่าการทดลองนี้ จะเป็นการทดลองที่หาความเร่งโน้มถ่วงได้ไม่แม่นยำนัก
แต่อยากทราบว่า วิธีการใดจะเป็นวิธีวัด/ทำการทดลองที่ดีที่สุดอะครับ
1) วัดคาบของการแกว่ง 20T (เป็นตัวเลขอื่นก็ได้ครับ, แต่มากกว่านี้ก็เริ่มเบื่อ) ที่ความยาว L ต่างๆ และหาค่า g ของแต่ละชุดข้อมูล ก่อนจะนำมาเฉลี่ย
2) ทำเช่นเดียวกับ ข้อ 1 แต่หาค่า g โดยอาศัยความชันของกราฟ T^2 กับ L (จากการวาดกราฟ/regressionด้วยcom/เครื่องคิดเลข)
3) วัดคาบการแกว่ง 20T ของการแกว่งที่ความยาว L เท่าเดิม หลายๆครั้ง แล้วนำมาเฉลี่ย หาค่า g
4) วัดคาบการแกว่ง 200T ของการแกว่งที่ความยาว L ค่าเดียวแล้วนำมาหาค่า g
5) วัดคาบการแกว่ง 20T ที่ความยาว L เท่าเดิม คล้ายข้อ 3) แต่ปล่อยให้ลูกต้มแกว่งไปเรื่อย (คล้ายกับในข้อ4)
นั่นคือ บันทึกเวลาที่ 20T, 40T, 60T, ..., 200T แล้วนำแต่ละช่วงมาลบกัน เฉลี่ยหาคาบ T แล้วหาค่า g

วิธีไหนดีที่สุดอะครับ ช่วยอธิบายเหตุผลสั้นๆ (ไม่ต้องยาวมาก) เป็นสมการหรือเป็น%ความคลาดเคลื่อนด้วยก็ได้ครับ
ขอขอบคุณล่วงหน้าครับ
ต่อท้าย #1 13 ก.พ. 2553, 19:14:26
ที่สงสัยเพราะว่า ประเทศญี่ปุ่น นิยมทำแบบที่ 5 ครับ
ต่อจากที่คุณ Lugia ตอบมาครับ
เมื่อเวลาผ่านไปลูกต้มอาจแกว่งเร็วขึ้นเล็กน้อยครับ เพราะมีมุมมีขนาดเล็กลงเนื่องด้วยแรงเสียดทานที่่จุดหมุน
ตอบ ข้อ 2. ไม่ขึ้นอยู่กับมวลของลูกต้ม

สืบค้นข้อมูล
ให้พิรารณารูปแต่ละรูป ซึ่งเป็นการเคลื่อนที่ของวัตถุ ในเงื่อนไขต่างๆ กัน  จากการเคลื่อนที่ จะแสดงแถบกระดาษ ของการเคลื่อนที่ และกราฟของการกระจัด ความเร็ว ความเร่งกับเวลา ของการเคลื่อนที่ตามเงื่อนไขดังกล่าว

   

รูปที่ 1 แสดงแถบกระดาษของวัตถุที่เคลื่อนที่ด้วยความเร็วคงที่ โดยมีทิศทางไปทางซ้าย  
วัตถุชิ้นหนึ่งเคลื่อนที่จากหยุดนิ่งด้วยอัตราเร็วคงที่ไปทางซ้ายมือ     เมื่อนำแถบกระดาษที่สอดผ่านเครื่องเคาะสัญญาณเวลา มาพิจารณา จะได้ ลักษณะของจุดบนแถบกระดาษ ดังรูป 1(บน) จากแถบกระดาษพบว่าระยะห่างระหว่างช่วงจุดจะเท่า ๆ กัน(แสดงว่าอัตราเร็วคงที่) ระยะการกระจัดของวัตถุจะเป็นลบเพิ่มมากขึ้นเรื่อย ๆ (ให้ทิศไปทางขวามือเป็นบวก) และเมื่อนำระยะห่างบนจุดกระดาษไปเขียนกราฟระหว่างการกระจัดกับเวลาจะได้กราฟรูปซ้ายมือ เส้นกราฟมีลักษณะของเส้นตรงซึ่งสามารถหาความชันได้ โดยความชันก็คือความเร็วของการเคลื่อนที่ ซึ่งเป็นความเร็วที่คงที่(กราฟรูปกลาง)   โดยความเร็ว จะเป็นลบ มีค่า = -12 m/s และกราฟความเร่งกับเวลา(รูปขวามือ)เร่งเท่ากับศูนย์ตลอดเวลาการเคลื่อนที่
 

   

 รูปที่ 2 แสดงแถบกระดาษของวัตถุที่เคลื่อนที่ด้วยความเร่งคงที่ ไปทางขวามือ  
วัตถุชิ้นหนึ่งเคลื่อนที่จากหยุดนิ่งด้วยความเร่งคงที่ไปทางขวามือ เมื่อนำแถบกระดาษที่สอดผ่านเครื่องเคาะสัญญาณเวลา มาพิจารณา จะได้ ลักษณะของจุดบนแถบกระดาษ ดังรูป 2(บน)พบว่าระยะห่างระหว่างช่วงจุดแต่ละช่วงจะไม่เท่ากันแต่จะเพิ่มมากขึ้นเรื่อย ๆ หมายความว่าระยะทางที่เคลื่อนที่ได้ใน 1 หน่วยเวลาจะมากขึ้นเรื่อย ๆ เมื่อเวลาเพิ่มขึ้น และเมื่อนำระยะห่างบนจุดกระดาษไปเขียนกราฟระหว่างตำแหน่งของวัตถุกับเวลา จะได้ดังกราฟในลักษณะกราฟพาราโบล่าดังรูปที่ 2 (ล่างซ้าย)   ซึ่งสามารถหาความชันที่เวลาต่าง ๆ (จากความชันของเส้นสัมผัสส่วนโค้งที่เวลาต่าง ๆ)ได้ พบว่าความชันเพิ่มขึ้นอย่างสม่ำเสมอและมีค่าเป็นบวก แต่ค่าของความชันก็คือความเร็ว นั่นแสดงว่าความเร็วของวัตถุจะเพิ่มขึ้นอย่างสม่ำเสมอและมีค่าเป็นบวก (ดูกราฟรูปกลาง) และความเร่งของวัตถุหาได้จากความชันของเส้นกราฟความเร็วกับเวลา(กราฟเส้นตรงจะมีความชันคงที่) กราฟความเร่งกับเวลา(รูปซ้ายมือ) จะพบว่ามีค่าคงที่เท่ากับ +1.5เมตร/วินาที2  

 
 รูปที่ 3 แสดงแถบกระดาษของวัตถุที่เคลื่อนที่ด้วยความคงที่(ความเร่งเป็นลบ) ไปทางขวามือ  
 วัตถุชิ้นหนึ่งเคลื่อนที่ด้วยความเร็วต้น 20 m/s ด้วยความเร่งคงที(แต่เป็นลบ)่ไปทางขวามือ เมื่อนำแถบกระดาษที่สอดผ่านเครื่องเคาะสัญญาณเวลา มาพิจารณา จะได้ ลักษณะของจุดบนแถบกระดาษ ดังรูป 3(บน)  จากแถบกระดาษพบว่าระยะห่างระหว่างช่วงจุดแต่ละช่วงจะไม่เท่ากันแต่จะลดลงเรื่อย ๆ หมายความว่าระยะทางที่เคลื่อนที่ได้ใน 1 หน่วยเวลาจะลดลงเรื่อย ๆ เมื่อเวลามากขึ้น เมื่อนำมาเขียนกราฟระหว่างการกระจัดของวัตถุกับเวลา พบว่าการกระจัดของวัตถุจะเพิ่มขึ้นเรื่อย ๆ  แต่อัตราการเพิ่มขึ้นในแต่ละช่วงเวลาจะลดลงเรื่อย ๆ  โดยมีการเปลี่ยนแปลงในลักษณะกราฟพาโบล่า(คว่ำ) ดังกราฟรูปที่ 3 (ล่างซ้าย) ซึ่งสามารถหาความชันที่เวลาต่าง ๆ (จากความชันของเส้นสัมผัสส่วนโค้ง)ได้ พบว่าความชันลดลงอย่างสม่ำเสมอ แตยังคงมีค่าเป็นบวก และค่าของความชันก็คือความเร็ว นั่นแสดงว่าความเร็วของวัตถุจะลดลงอย่างสม่ำเสมอ(แต่ค่ายังเป็นบวก) (ดูกราฟรูปกลาง) และความเร่งของวัตถุหาได้จากความชันของเส้นกราฟความเร็วกับเวลา(ซึ่งเป็นกราฟเส้นตรงจะมีความชันคงที่) กราฟความเร่งกับเวลา(รูปซ้ายมือ) จะพบว่ามีค่าคงที่และเป็นลบ -0.75 เมตร/วินาที2
 

 รูปที่ 4 แสดงแถบกระดาษของวัตถุที่เคลื่อนที่ด้วยความเร่งคงที่ ไปทางซ้าย
วัตถุชิ้นหนึ่งเคลื่อนที่จากหยุดนิ่งด้วยความเร่งคงที่ไปทางซ้ายมือ เมื่อนำแถบกระดาษที่สอดผ่านเครื่องเคาะสัญญาณเวลา มาพิจารณา จะได้ ลักษณะของจุดบนแถบกระดาษ ดังรูป 4(บน) และเมื่อนำระยะห่างบนจุดกระดาษไปเขียนกราฟระหว่างตำแหน่งของวัตถุกับเวลา จะได้ดังกราฟรูปที่ 4 กราฟซ้ายมือแสดงการกระจัดของวัตถุกับเวลา พบว่าการกระจัดมีการเปลี่ยนแปลงในลักษณะกราฟพาโบล่า(แต่อยู่ใต้แกน) ซึ่งสามารถหาความชันที่เวลาต่าง ๆ (จากความชันของเส้นสัมผัสส่วนโค้ง)ได้ พบว่าความชันเพิ่มขึ้นอย่างสม่ำเสมอและมีค่าเป็นลบ(เป็นลบมากขึ้นเรื่อย ๆ) แต่ค่าของความชันก็คือความเร็ว นั่นแสดงว่าความเร็วของวัตถุจะเพิ่มขึ้นอย่างสม่ำเสมอและมีค่าเป็นลบ (ดูกราฟรูปกลาง) และความเร่งของวัตถุหาได้จากความชันของเส้นกราฟความเร็วกับเวลา(ซึ่งเป็นกราฟเส้นตรงจะมีความชันคงที่) กราฟความเร่งกับเวลา(รูปซ้ายมือ) จะพบว่ามีค่าคงที่เท่ากับ - 1.5เมตร/วินาที2  
ให้พิจารณารถ 3 คัน จงพิจารณาว่ารถคันใดเคลื่อนที่อย่างไร คันสีใดมีความเร็วคงที่ มีความเร่งเป็นบวก และมีความเร่งเป็นลบ
(หมายเหต รถแต่ละคันไม่ได้เคลื่อนที่จากหยุดนิ่ง)

 
  รูปที่ 5 แสดงการเคลื่อนที่ของรถ 3 คัน มีความเร่งไม่เท่ากัน
1. รถสีแดงเคลื่อนที่ด้วยความเร่งเป็นลบ   ทำให้ความเร็วรถลดลงอย่างสม่ำเสมอ  (สังเกต ได้จากการเคลื่อนที่ช้าลง) อาจเรียกความเร่งประเภทนี้ว่า ความหน่วง ในการคำนวน จะกำหนดให้ความเร่งประเภทนี้มีเครื่องหมายลบ 2. รถสีเขียวเคลื่อนที่ด้วยความเร็วคงที่ ซึ่งแสดงว่าความเร่งเท่ากับศูนย์
3. รถสีน้ำเงินเคลื่อนที่ด้วยความเร่งเป็นบวก    ทำให้ความเร็วรถเพิ่มขึ้นอย่างสม่ำเสมอ      ในการคำนวนจะกำหนดให้ความเร่งประเภทนี้ มีเครื่องหมายบวก 
 
้พิจารณาการเคลื่อนที่ของรถ 2 คัน เคลื่อนที่ด้วยความเร็วไม่เท่ากัน เริ่มต้นเคลื่อนทีไม่ พร้อมกัน คันสีแดงวิ่งมาด้วยความเร็วคงที่ 20 m/s ผ่านคันสีน้ำเงินซึ่งเคลื่อนที่ด้วยความเร็ว 5.5 m/s ณ ตำแหน่ง 20 เมตร จากจุดอ้างอิง  สามารถเขียนกราฟได้ดังรูป
 
 

รูปที่ 6 แสดงการเคลื่อนที่ของรถ 2 คัน ด้วยความเร็วไม่เท่ากัน ออกจากจุดเดียวกัน
้
พิจารณาการเคลื่อนที่ของรถ 2 คัน เคลื่อนที่ด้วยความเร็วไม่เท่ากัน ออกจากจุดเริ่มต่างกัน เมื่อเขียนกราฟระหว่างตำแหน่งของรถแต่ละคันกับเวลา ได้ดังกราฟ
 
รูปที่ 7 แสดงการเคลื่อนที่ของรถ 2 คัน ด้วยความเร็วไม่เท่ากัน จากจุดเริ่มต้นต่างกัน
     รถคันสีฟ้าเคลื่อนที่ด้วยอัตราเร็วคงที่ 6 m/s จากตำแหน่งที่ 20      รถคันสีแดงเคลื่อนที่ด้วยความเร็วคงที่ 16.67 m/s และเริ่มเคลื่อนที่จากตำแหน่งอ้างอิง      ข้อสังเกตโดยรถทั้ง 2 คันเริ่มต้นเคลื่อนที่ไม่พร้อมกัน

พิจารณาการเคลื่อนที่ของรถ 2 คัน เคลื่อนที่ด้วยความเร็วไม่เท่ากัน ออกจากจุดเริ่มต้นเดียวกัน เมื่อเขียนกราฟระหว่างความเร็วกับเวลาของรถทั้งสองได้ดังรูป
 
 
รูปที่ 8 แสดงการเคลื่อนที่ของรถ 2 คัน ด้วยความเร็วไม่เท่ากัน จากจุดเริ่มต้นเดียวกัน
     รถคันสีฟ้าเคลื่อนที่ด้วยอัตราเร็วคงที่ 10 m/s      รถคันสีแดงเคลื่อนที่ด้วยความเร่งคงที่ 4.2 m/s2 เป็นเวลา 3 วินาที หลังจากนั้นจะเคลื่อนที่ด้วยความเร็งคงตัว      ข้อสังเกตุโดยรถทั้ง 2 คันเริ่มต้นเคลื่อนที่พร้อมกัน
ตอบ ข้อ 4. ระยะทางเพิ่มขึ้นสม่ำเสมอ

ที่มา http://www.rmutphysics.com/physics/oldfront/73/1/motion.htm
สืบค้นข้อมูล

โปรเจคไตล์ขอให้ทำความเข้าใจว่า การเคลื่อนที่แบบนี้เกิดบนสมมุติฐานที่ว่า การเคลื่อนที่ในแกน X และการเคลื่อนที่ในแนวแกน Y แยกจากกัน ทำให้เวลาคิด ก็แค่คิดแบบต่างคนต่างไปก็พอ
นี่คือรูป การเคลื่อนที่แบบโปรเจคไตล์นะครับ

ภาคคำนวน
ก่อนอื่นเราต้องรู้วิธีการแตกเวกเตอร์ก่อน ในรูปนั่นอ่ะ แตกเวกเตอร์ของความเร็วได้อะไร ในแนวแกน X และ Y
แกน X คือ แกนนอน แกน Y คือแกนตั้งนะครับ
โดยทั่วไป เค้าก็จะจำกันว่า ชิดมุมใช้คอส ห่างมุมใช้ไซน์
หมายถึง ถ้าเป็นความเร็วในแนวที่ชิดกับมุม ดูจากในรูป คือแกน X ก็จะใช้ เวกเตอร์ที่จะแตก(U)แล้วคูณด้วย cos จากตัวอย่าง ถ้าห่างมุมก็จะใช้ U คูณด้วย sin
จากตัวอย่างความเร็วในแนวแกน X ก็คือ U cos เซต้า   แกน Y ก็คือ U sin เซต้า
ความจริงเราสามารถพิสูจน์ได้ไม่ยาก ว่าแตกแล้วทำไมถึงได้แบบนั้น ใช้ตรีโกณง่ายๆ
ลองไปทำดูเองนะครับ มันหารูปที่จะทำให้ดูยากอ่ะ ขอข้ามไปแล้วกัน

ทีนี้เวลาทำโจทย์อ่ะ ก็ต้องแยกความเร็วคิดก่อนเลย แตกเวกเตอร์แบบข้างบนแหละ ให้ได้ความเร็วออกมาทั้งแกน X และแกน Y
ลองดูอันนี้นะ
เวลาคิดก็คอนเซปเดิม คือ แยกคิดแต่ละแกน ซึ่งแต่ละแกนนั้นอ่ะ จะเชื่อมกันด้วยเวลา
ประมาณว่า ผ่านไป 1 วิ มันขึ้นไปในแกน Y แต่ 1 วินั้นมันก็ไปทางขวา ของแกน X ด้วยเช่นเดียวกัน
เพราะ งั้นเรื่องนี้ก็จะเซตได้ 2 สมการ ที่เชื่อมกันด้วย เวลา(t) โดยแกน X จะง่ายๆ ไม่มีไรซับซ้อน เนื่องจาก มันไม่โดนความเร่งกระทำ เริ่มมามันมีความเร็วเท่าไหร่ มันก็ไปด้วยความเร็วนั้นต่อไปเรื่อยๆ
(ความเร่งที่กระทำกับวัตถุ อยู่ในแนวแกน Y) จากสมการ s = ut + 1/2at2 แต่ a เป็น 0 ก็จะทำให้เหลือ
แค่ s = uxt (U ต้องเป็น ความเร็วในแนวแกน X)เพราะงั้นถ้าเราจะหาระยะทางที่ไปได้ ก็ต้องการแค่ความเร็วในแกน X กับเวลาก็พอแล้ว
แต่...
แต่... เวลา ที่แกน X ใช้ในการเคลื่อนที่ในเรื่องนี้คืออะไร ลองดูรูป แล้วคิดตามว่า แกน X จะเริ่มวิ่งเมื่อไหร่ (ก็ตอนมันเริ่มขึ้นอ่ะจิ) แล้วมันจะหยุดวิ่งเมื่อไหร่(ก็ตอนที่มันปักลงพื้นอ่ะจิ หัวทิ่มดินแล้ว มันก็ไม่วิ่งต่อ)
เพราะงั้น เวลาที่แกน X ใช้เคลื่อนที่ก็คือ เวลาที่ แกน Y ใช้เริ่มขึ้นข้างบน แล้วตกลงพื้นนั่นเอง
ถ้า โจทย์เป็นแบบนี้ก็ไม่มีอะไรมาก ก็แค่คิดหาเวลาที่มันใช้ตกลงพื้น(ใช้การ เคลื่อนที่แนวดิ่งแล้ว เห็นไม๊ ก็คือการกระจัดเป็น 0 และความเร็วเริ่มต้นที่ใช้ก็ต้องเป็นความเร็วที่แตกเข้าแกนแล้ว) แล้วก็นำเวลานั้นไปแทนค่าใน สมการของแกน X (บอกแล้วว่ามันเชื่อมกันด้วยเวลา) แล้วก็ตอบ

โจทย์ทดสอบความเข้าใจนะครับ

ขว้าง ลูกบอลออกจากตึกสูง 500 เมตร ด้วยความเร็ว 100 m/s ในแนวทำมุมเงย 30 องศากับแนวราบ จงหาว่าขณะที่ลูกบอลกระทบพื้น จะมีความเร็วเท่าใด และตกห่างจากจุดเริ่มปล่อยเท่าไรในแนวระดับ

เริ่มกันที่เราต้องแตกความเร็วออกไปในแกน X และ Y ได้ว่า U(x) = 50รูท3 m/s (หาวิธีพิมพ์ไม่ได้อ่ะ) U(y) = 50 m/s
ที นี้ โจทย์บอกว่าวัตถุ มันร่วงลงไปจากตึก กระทบพื้น เราก็จะมาหาเวลาที่มันใช้ร่วงไปยังพื้น(ซึ่งเวลานั้นแหละที่ความ เร็วในแกน X ใช้พาลูกบอลไปในแนวระดับ) จากสมการ s = ut +1/2at2(ใคร ที่ยังงงว่า เลือกสูตรไหนมาใช้หว่า ขอแนะนำว่าให้ตั้งมั่นไว้ว่าเราต้องการอะไร แล้วดูว่า เรารู้อะไรบ้าง ทำไปซักพัก มันจะเลือกสูตรได้เอง)
มันร่วงลงไปการกระจัดเป็น -500 m ความเร็วมีทิศขึ้นเพราะงั้นเป็น +50 m/s ค่า g มีทิศลงเพราะงั้นมีค่าเป็น -10m/s แก้สมการ -500 = 50t - 5t2 เสร็จแล้วก็แก้หา t ได้จาก การแก้สมการกำลังสอง ได้ t ออกมาไม่สวยนัก(เลขห่วย) แล้วเอาเวลา t นั้นอ่ะ ไปคูณกับความเร็วในแกน X ก็จะได้คำตอบของระยะทางที่โจทย์ต้องการ
ส่วนความเร็ว ที่จุดกระทบนั้นก็ให้หาความเร็วในแกน y ตอนที่กำลังจะกระทบพื้น
ซึ่งหาได้จากสูตร v2 = u2 +2as แทนค่า(ไม่ลงรายละเอียดแล้วนะครับ)
ก็จะได้ v2 = 7500 + 2 *-10*-500 = 7500+10000 = 17500
แต่ เราจะถอดรูทเลย แล้วตอบ ก็คงง่ายไป เค้าจะหลอกตรงที่ว่า ความเร็วที่ตกกระทบพื้น หลักๆ เกิดจาก แกน y ก็จริง แต่ในข้อนี้ ต้องเอาแกน X มารวมด้วย
รวมเวกเตอร์ได้ว่า 17500+2500 = v2 = 20000
ถอดรูทออก ก็จะได้ 100รูท2 เป็นคำตอบสุดท้ายในบทนี้

ตอบ ข้อ 3. ความเร็วของวัตถุในแนวดิ่งที่เป็นศูนย์



สืบค้นข้อมูล
ความหมายของอัตราเร่งหรือความเร่ง คือ อัตราเร็วหรือ ความเร็วที่เปลี่ยนไปในหนึ่งหน่วยเวลาที่วัตถุมีการเคลื่อนที่
               การคำนวณหาค่าอัตราเร่ง ทำได้โดยหาอัตราเร็วที่เปลี่ยนไปโดยใช้อัตราเร็วสุดท้ายของการเคลื่อนที่ลบด้วยอัตราเร็วเริ่มต้นของการเคลื่อนที่ หารด้วยเวลาที่ใช้เปลี่ยนค่าอัตราเร็วนั้น เช่น
               กำหนดให้        เป็นอัตราเร็วเริ่มต้นของการเคลื่อนที่
                                       เป็นอัตราเร็วสุดท้ายของการเคลื่อนที่
                                      เป็นเวลาขณะที่เริ่มต้นการเคลื่อนที่
                                      เป็นเวลาในช่วงสุดท้ายของการเคลื่อนที
                                       เป็นค่าอัตราเร่งของการเคลื่อนที่
                สมการแสดงความสัมพันธ์ คือ
                         หรือ                                  ถ้า  คือ ช่วงเวลาที่มีการเปลี่ยนค่าอัตราเร็ว   (สมการที่ 2)
               สำหรับสูตรในการคำนวณหาค่าความเร่ง  ใช้สูตรเดียวกัน เพียงแต่ค่าความเร็วที่เปลี่ยนไปเป็นปริมาณสเกลลาร์

ตอบ ข้อ 1.  1.6 m/s



สืบค้นข้อมูล

อัตราเร็วเฉลี่ย

อัตราเร็วในรูป สมบัติเชิงกายภาพ มักแทนอัตราเร็วที่ขณะใดขณะหนึ่ง ในชีวิตจริงเรามันใช้ อัตราเร็วเฉลี่ย (ใช้สัญลักษณ์ \tilde{v}) ซึ่งก็คือ อัตรา ของ ระยะทาง รวม (หรือ ความยาว) ต่อช่วง เวลา
ยกตัวอย่างเช่น ถ้าคุณเคลื่อนที่ได้ 60 ไมล์ในเวลา 2 ชั่วโมง อัตราเร็ว เฉลี่ย ของคุณในช่วงเวลานั้นคือ 60/2 = 30 ไมล์ต่อชั่วโมง แต่อัตราเร็วที่ขณะใดขณหนึ่งย่อมเปลี่ยนแปลงต่างกันไป
ในรูปสัญลักษณ์ทางคณิตศาสตร์

\tilde{v} = \frac{\Delta l}{\Delta t}.
อัตราเร็วที่ขณะใดขณะหนึ่งซึ่งนิยามเป็นฟังก์ชันของ เวลา ในช่วงเวลา [t0,t1] จะให้อัตราเร็วเฉลี่ยในรูป
\tilde{v} = \frac{\int_{t_0}^{t_1} v (t) \, dt}{\Delta t}
ในขณะที่อัตราเร็วที่ขณะใดขณะหนึ่งซึ่งนิยามเป็นฟังก์ชันของ ระยะทาง (หรือ ความยาว) ในช่วงความยาว [l0,l1] จะให้อัตราเร็วเฉลี่ยในรูป
\tilde{v} = \frac{\Delta l}{\int_{l_0}^{l_1} \frac{1}{v (l) } \, dl}
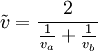
บ่อยครั้งที่มีคนคาดโดยสัญชาตญาณ แต่ผิด ว่าการเคลื่อนที่ครึ่งแรกของระยะทางด้วยอัตราเร็ว va และระยะทางครึ่งที่สองด้วยอัตราเร็ว vb จะให้อัตราเร็วเฉลี่ยรวมเป็น \tilde{v} = \frac{v_a + v_b}{2} ค่าที่ถูกต้องต้องเป็น \tilde{v} = \frac{2}{\frac{1}{v_a} + \frac{1}{v_b}}
(ระลึกไว้ว่า อย่างแรกเป็น ค่าเฉลี่ยเลขคณิต ในขณะที่อย่างที่สองเป็น ค่าเฉลี่ยฮาร์มอนิก)
อัตราเร็วเฉลี่ยสามารถหาได้จาก distribution function ของอัตราเร็วได้เช่นกัน (ทั้งในรูประยะทางหรือเวลาก็ตาม)
v \sim D_t\; \Rightarrow \; \tilde{v} = \int v D_t (v) \, dv
v \sim D_l\; \Rightarrow \; \tilde{v} = \frac{1}{\int \frac{D_l (v) }{v} \, dv}
ตอบ ข้อ 3.  2.0 m/s

ที่มา http://th.wikipedia.org/wiki/%E0%B8%AD%E0%B8%B1%E0%B8%95%E0%B8%A3%E0%B8%B2%E0%B9%80%E0%B8%A3%E0%B9%87%E0%B8%A7


สืบค้นข้อมูล
ประจุไฟฟ้า มี 2 ชนิด คือ ประจุไฟฟ้าบวก แทนด้วยเครื่องหมาย +  และประจุไฟฟ้าลบ  แทนด้วยเครื่องหมาย  -
ประจุบวกที่มีขนาดเล็กที่สุดคือ โปรตอน มีประจุ +1.6 x 10-19 C มีมวล 1.67 x 10-27 kg
ประจุลบที่มีขนาดเล็กที่สุดคือ อิเลคตรอน มีประจุ -1.6 x 10-19 C มีมวล 9.1 x 10-31 kg
โปรตอนมีประจุไฟฟ้าเท่ากับอิเลคตรอนแต่เป็นชนิดตรงกันข้าม และมีมวลมากว่าอิเลคตรอน ประมาณ 1800 เท่า
โดยในสภาวะปกติอะตอมจะเป็นกลางทางไฟฟ้า  คือมีจำนวนประจุไฟฟ้าบวกเท่ากับจำนวนประจุไฟฟ้าลบ

วัตถุโดยทั่วไป แบ่งได้ 2 ชนิด คือ
        ตัวนำ  หมายถึงวัตถุที่สามารถนำไฟฟ้าได้ ยินยอมให้ประจุไฟฟ้าเคลื่อนที่ผ่านวัตถุนี้ได้
        ฉนวน หมายถึงวัตถุที่ไม่ยินยอมให้ประจุไฟฟ้าเคลื่อนที่ผ่านได้ ถ้าเราให้ประจุแก่ฉนวนประจุนั้นจะอยู่นิ่งกับที่ไม่เคลื่อนที่ไปไหน

ตอบ ข้อ 4. ทิศ -Y ด้วยความเร่ง

ที่มา http://www.pt.ac.th/ptweb/prajead/electric/ststics/conductor/force.htm
สมัครสมาชิก: บทความ (Atom)